Certainties, probabilities and possibilities
Who needs Ronaldo and Mbappé when you have the big lad Data Science in your team?
Euro 2020 has reached the 3rd round of group stage matches. Some teams are already through to the knockouts but others have it all still to do.
Based on results so far and form coming into the Euros, we have run a model to predict the outcome of the final group stage matches. From these we have worked out the probability of where in the group each team will finish and who goes through as winners, runners up or one of the four best 3rd placed teams (taking points and goal difference into account).
Group A
Italy has already qualified for the knockouts and have 89% probability of topping the group (by not losing to Wales).
Wales are almost certain to qualify and has a 78% probability of finishing second. They could finish as low as 3rd if they lose against Italy and Switzerland beat Turkey but would almost certainly still qualify in this scenario.
Switzerland has a 70% probability of finishing 3rd but could finish second if they win and Wales lose and have a better goal difference than the Welsh. Our model suggests that this scenario is unlikely as it gives only an 11% probability of this outcome.
For Turkey the mathematics are quite simple: If they don't beat Switzerland they go home. In fact, the model thinks they are going home anyway as they have an 81% probability of finishing bottom of the group.
Group B
Belgium is already through and has a 94% probability of topping the group. They will do this with a win or draw against Finland. Belgium's qualification is the only certainty in this group.
Denmark and Russia play each other and this throws up different possibilities for final placings. Russia has a 45% probability of finishing 2nd but a 50% probability of finishing bottom. Denmark, which has lost both of its games, could finish 2nd if they win and Finland lose and have the best goal difference in the three way head-to-head. Our model gives this a 36% chance of happening.
A win or a draw for Russia and a Finland loss or draw will see Russia through.
Depending upon results Finland could finish 1st, 2nd or 4th but it is more likely that they will finish 3rd (75% probability) but this may not be enough to get them through as one of the best placed 3rd teams.
Group C
Netherlands are through as group winners.
Ukraine has a 74% probability of finishing 2nd. To do this they have to win or draw against Austria.
If Austria beat Ukraine they will finish 2nd, there is a 26% probability of this happening with 3rd place (74% probability) being there most likely outcome for the Austrians.
North Macedonia can only finish 4th.
Group D
There is a 60% probability that England will top the group by beating the Czech Republic. Draw and they finish 2nd. There is 2% chance that England finish 3rd. For this to happen England would need to lose their match and Scotland beat Croatia by a big enough score to mean that they go above England on goal difference. Even so, England are almost certain to qualify for the knockouts (99% probability).
The Czech Republic also has a 99% probability of qualifying. A win or a draw against England will see them top the group.
Scotland has a 32% probability of qualifying but they must win against Croatia to be in with a chance. The bigger the margin of victory the greater the chance.
Our model gives Croatia a 53% probability of finishing 3rd and a 32% chance of 4th. It is still possible for them to finish 2nd but it requires England to beat Czech Republic, Croatia to beat Scotland and Croatia's goal difference to be better than the Czech's. The probability of this outcome is 15%.
Group E
This is a tight group with both Spain and Sweden having the best chance of winning the group. Both are likely to qualify as Sweden has a 98% probability and Spain 87% of finishing either in the top two or as one of the best 3rd placed countries.
Poland could still finish in a top 3 position, however our model thinks this unlikely and gives Poland a 63% probability of finishing 4th.
If Slovakia beat Spain they will be through, or if they draw and Sweden don't lose.
Group F
This is another tight group.
France has almost certainly qualified (99% likely to get through to the knockouts) and has a 49% probability of winning the group. To do this they need to beat Portugal or draw and hope Germany do not beat Hungary.
Germany will also qualify (96% probability) and win the group if they beat Hungary and France do not win against Portugal. The model predicts a 47% probability of this outcome. There is a 45% probability that Germany will finish 2nd.
Portugal has a 72% probability of finishing 3rd but could still get 2nd (22% probability). There is also a scenario that sees the current holders eliminated in 4th if they lose to France and Hungary beat Germany. Don't get too excited though - the model predicts a 2% probability for this outcome. In fact, Portugal has an 87% probability of qualifying either by finishing in the top two or as one of the best 3rd placed countries.
Hungary are still in with a chance going into the final group match. They finish second if they beat Germany and Portugal lose but the probability of this outcome is only 2%. There is a 94% probability that Hungary will finish 4th.
Qualifying as best 3rd placed team
In Euro 2020, the top two from each group go through to the knockout stage along with the four best 3rd placed teams. These four are determined by the highest points and then goal difference if two or more teams are tied on points. If teams cannot be separated by goal difference then goals scored, number of wins and finally disciplinary record can come into play.
The key question is what combination of points and goal difference will be enough to see a country through to the knockouts as one of the best 3rd placed teams?
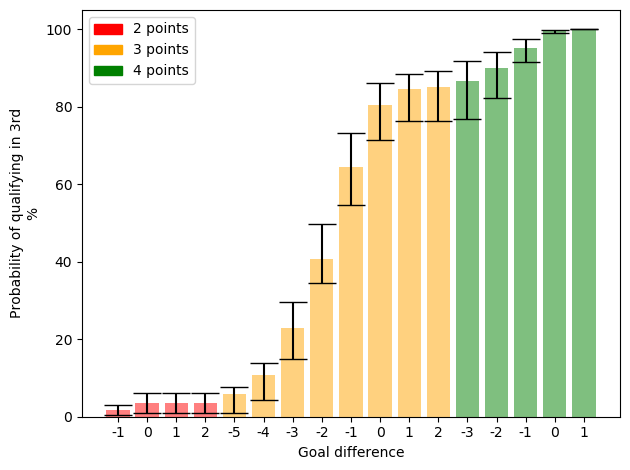
We've modelled the probabilities for a number of points and goal differences for teams finishing in 3rd place and plotted them on the graphic below. In each group the probabilities are slightly different, as a result we have marked the bottom and top of the range (denoted by the lines) and the average (as shown by the bars).
Probabilities for qualifying for the knockouts associated with each combination of points and goal difference for 3rd placed teams
The graphic shows that a team in 3rd place is unlikely to qualify without getting at least 3 points and having a goal difference of no worse than -1. This combination gives a 3rd place team an average of 64% probability of qualifying. Having a goal difference that is inferior by just one goal reduces the probability of qualifying to around 41%.
A country with three points and a goal difference of 0 has around an 81% probability of qualifying. A team finishing in 3rd with four points with a -2 goal difference has on average a 90% chance of qualifying. This is why we can say that Wales (on 4 points +2 goal difference) has almost certainly qualified for the knockouts regardless of what happens in their final game. Some groups are more competitive than others which means that 3rd placed teams will pick up more points and have a better goal difference than 3rd placed teams in other groups.
The graphic below gives further insight into the strength of each group. Teams from group F are most likely to qualify in 3rd and teams from group B are least likely to qualify. Teams from group F are more likely to finish in third with a higher number of points and a greater goal difference (the opposite is true for group B). These two groups are also responsible for the upper and lower limits respectively in the graphic showing points and goal difference combinations, as the weaker teams have to face a stronger level of opposition relatively, so even if they achieve greater points totals and goal difference than expected there is more chance another 3rd place team can still finish ahead of them.
Probability of qualifying in 3rd place by group
Teams most likely to qualify in third come from Group F, Group C, Group D and Group E.
However, there is another factor which makes it more likely teams from these groups will qualify in third - they are more likely to know what score they need to ensure qualification.
Euro 2020 is not a fair competition
The results in one group affect the number of points and goal difference needed for the teams in the other groups and unlike the last game of the season in the Premier league, the final game of the groups are not all played at the same time. Group A plays first followed by C,B,D,E and finally F.
This gives a strategic advantage to the teams playing later because they know exactly what they need to do to ensure qualification.
Which countries will qualify for the knockouts?
Taking all of this analysis into account we think that the following teams will qualify for the knockout stages.
You will see that for two groups there is an either/or given. Obviously, we would like Scotland to get through from group D but Croatia have a slightly higher probability of qualifying. In group E Slovakia have a slightly higher probability than Poland.
For more data science at the Euros go here.